네오의 귀걸이

귀걸이를 좋아하는 네오는 자신만을 위한 귀걸이를 만들기로 하였다. 기하학적으로 아름다운 귀걸이를 만들고 싶던 네오는 아래와 같은 모습의 귀걸이를 구상 중이다.

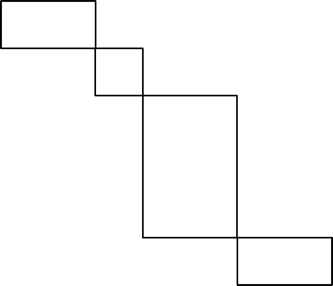
2차원 좌표 평면에 N개의 점이 주어져 있다. 점들의 x나 y 좌표가 겹치는 경우는 없다고 하자. 이들 점 중 가장 왼쪽에 위치한 점은 항상 가장 위쪽에 위치한 점과 같다. 이 점을 S라고 부르자. 마찬가지로, 가장 오른쪽에 위치한 점은 항상 가장 아래쪽에 위치한 점과 같다. 이 점을 E라고 부르자.
기하학적으로 아름다운 귀걸이는 다음의 조건을 만족해야 한다. 주어진 점들을 왼쪽 위와 오른쪽 아래 꼭짓점으로 가지는 축에 평행한 직사각형들이 순서대로 놓여있다. 이때, 첫 번째 직사각형은 S를 왼쪽 위 꼭짓점으로 가져야 한다. 순서의 마지막 직사각형은 E를 오른쪽 아래 꼭짓점으로 가져야 한다. 순서에서, 어떤 직사각형 A 바로 다음에 직사각형 B가 등장한다면, A의 오른쪽 아래 꼭짓점은 B의 왼쪽 위 꼭짓점과 같은 점이어야 한다.
주어진 점 각각은 자신의 특징적인 k값을 가지고 있다. 이 값의 의미는 해당 점이 어떤 직사각형의 오른쪽 아래 점이 되는 경우 그 직사각형의 가로 폭과 세로 높이의 합이 정확히 k가 되어야 한다는 뜻이다.
네오는 주어진 점들로 만들 수 있는 기하학적인 귀걸이가 몇 가지인지 궁금하다. 또, 점을 하나 추가했을 때 혹은 점을 하나 제거했을 때의 종류도 몇 가지인지 궁금하다. 네오가 궁금증을 해결하기 위해 여러분의 도움이 필요하다.

S와 E는 처음상태에서 고정된다.
S와 E가 제거되는 경우와 추가되는 점이 일정한 영역을 벗어나는 경우에 주의하라.

입력 형식

입력은 점의 개수 n, 점의 정보를 담은 배열 point, 점의 추가 또는 삭제 정보를 담은 배열 query로 구성된다. point 배열은 n × 3 크기의 2차원 배열로, 각각의 행은 점의 x좌표, y좌표, 그리고 그 점의 k값으로 이루어져 있다. query 배열은 n × 4 크기의 2차원 배열로, 점을 추가하거나 삭제하는 변화의 정보를 담고 있다. 각 변화는 독립적으로 초기 상태에 대해서 적용됨에 주의하라. 즉, 변화가 누적되는 것이 아니다. 각 행의 첫 번째 값은 변화의 종류를 담은 값으로, 0인 경우 점을 추가하는 경우를 의미하고 1인 경우 최초에 주어진 n개의 점들 중 하나를 제거하는 경우를 의미한다. 점을 추가하는 경우는 새로 추가되는 점의 x좌표, y좌표, k값이 이후의 원소로 주어진다. 점을 삭제하는 경우는 삭제하려는 점의 x좌표, y좌표가 이후의 원소로 주어지며, 마지막 원소는 배열의 크기를 맞추기 위한 것으로 의미 없는 값이다. 제한조건은 다음과 같다.

• 2 <= n <= 100,000
• 주어진 점들 중 가장 왼쪽에 위치한 점은 항상 가장 위쪽에 위치한 점과 같음이 보장된다. 또한, 가장 오른쪽에 위치한 점은 항상 가장 아래쪽에 위치한 점과 같음이 보장된다.
• 추가되는 점은 최초에 주어진 점과 x좌표나 y좌표가 겹치지 않음이 보장된다. 제거되는 점은 최초에 주어진 점들 중 하나임이 보장된다. 모든 좌표 값은 -1,000,000,000 이상 1,000,000,000이하의 정수이다.

출력 형식

리턴 타입은 정수의 배열로, 총 n+1개의 원소로 이루어진 배열을 리턴한다. 첫 번째 원소는 초기 상태에서 가능한 기하학적 귀걸이의 개수를 1,000,000,007로 나눈 나머지여야 한다. 다음 n개의 원소는 각 변화에 대해 그 변화를 적용한 이후 가능한 귀걸이의 개수를 1,000,000,007로 나눈 나머지가 입력의 순서에 맞게 들어있으면 된다.

예제 입출력